Sign in Subscribe

Why grid is great!

Last updated on 
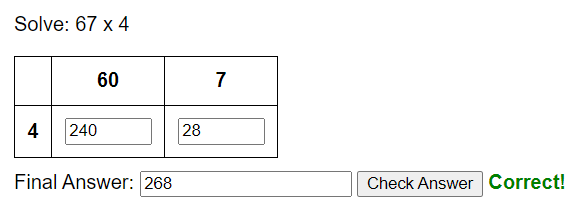
Grid method multiplication
Grid method multiplication

When it comes to teaching long multiplication, the grid method (or box method) often stands out as a particularly effective strategy. If you’ve been in the teaching world long enough, you’ve probably encountered several different approaches to multiplication. From the traditional algorithm to lattice multiplication, each method comes with its own strengths and quirks. But let me make the case for why the grid method deserves your attention—and why it just might be the most powerful tool you can use in the classroom.

Less Cognitive Demand: A Clearer Path to Understanding

One of the most compelling reasons to use the grid method is the reduced cognitive load it places on students. Traditional long multiplication requires students to juggle multiple mental processes at once—lining up digits correctly, carrying numbers, and keeping track of place values, all while ensuring accuracy. This can be a daunting task, especially for younger learners or those who struggle with working memory.

In contrast, the grid method breaks down multiplication into smaller, more manageable steps. The student only needs to multiply individual place values one at a time, filling in each box in the grid. Each small multiplication feels less overwhelming, and it allows students to focus on accuracy without feeling bombarded by too many tasks at once.

Because of this segmented approach, students aren't left scrambling to remember every little step. They can pause, check their work, and visually track their progress—this alone makes the grid method less cognitively demanding, allowing them to focus on what really matters: mastering multiplication itself.

A Visual Learning Experience

The grid method is a dream for visual learners. The multiplication process becomes spatial and organized, allowing students to see how each component of the problem fits into the larger whole. The boxes in the grid provide a scaffold for breaking down the multiplication process, making it much easier to conceptualize the relationship between numbers and their place values.

By visually arranging the calculations, the grid method ensures that no steps are missed and allows for a clearer sense of where numbers come from. The organization of the grid makes it hard to overlook important steps, which reduces careless mistakes that can happen with more abstract methods. This also fosters confidence in students who may feel intimidated by longer multiplication problems.

A Stepping Stone for Algebra

Another standout advantage of the grid method is its seamless transition into algebraic multiplication. Once students are comfortable with the grid for arithmetic, they can use the same framework when multiplying algebraic terms. This flexibility makes it an ideal tool for bridging the gap between arithmetic and algebra.

For example, if a student needs to multiply algebraic expressions like (x + 3)(x + 5), the grid method can easily accommodate this. The student can place each term into the grid, just as they would with numbers, and multiply the terms individually before summing them together. Not only does this process reinforce their understanding of multiplication, but it also introduces algebraic concepts like the distributive property in an intuitive way.

Reducing Anxiety in Struggling Learners

For students who struggle with math anxiety or have difficulty following multi-step processes, the grid method can be a real game-changer. The visual nature and step-by-step structure reduce the pressure of making mistakes. If they make an error in one small section of the grid, it doesn't ruin the entire problem. They can identify the issue, fix it, and continue with the process. This type of error resilience builds confidence and reduces anxiety over time.

Traditional long multiplication can feel like a make-or-break scenario, where one wrong move can lead to a cascade of mistakes. The grid method, on the other hand, empowers students to feel more in control, giving them the room to think critically without getting overwhelmed.

Real-World Applications

The grid method isn’t just a classroom tool—it mirrors the way we break down large tasks in real life. Whether you’re multiplying numbers in your head at the grocery store or tackling a complex engineering problem, breaking a larger problem into smaller parts is a fundamental skill. Teaching the grid method provides students with more than just a math strategy; it teaches them problem-solving skills that they will carry with them into adulthood.

Final Thoughts

At the end of the day, the goal of math education is to develop students who not only understand mathematical processes but also feel confident in using them. The grid method of long multiplication supports this by simplifying the process, reducing cognitive demand, and offering a visual, flexible, and intuitive approach. Whether you're helping students with basic multiplication or preparing them for the challenges of algebra, the grid method is a powerful and versatile tool that every math teacher should have in their toolkit.

Where next?

Why not give it a try now? We've currently got 4 different pages allowing your students to practise the grid method:

Subscribe now