Solving harder quadratics by factorising

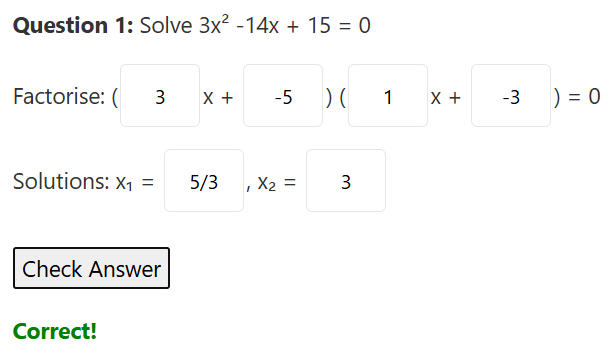
When solving harder quadratic equations you're tackling problems that come up in fields like physics, engineering, and even video game design. These equations help us model everything from the trajectory of a ball to the behavior of electrical circuits. By mastering these, you’ll unlock tools to analyze and solve more complex real-world problems! Jump to the questions

Practise now

For each quadratic equation, first factorise it (enter the four numbers for the factors) and then enter the two solutions. Answers must be integers or proper/improper fractions (like 1/2, -3/4, etc.).

Note: If you leave any factor coefficient box blank, it will be interpreted as 1.

Score: 0/8