Inverse proportion

Last updated on Sep 29, 2024

Inverse proportion screenshot

Inverse proportion is when one quantity increases as another decreases, and vice versa. This relationship is found in everyday scenarios like speed and travel time, or supply and demand. Understanding inverse proportion helps you solve problems where two quantities are inversely related, allowing you to predict how one affects the other. Jump to the questions

Practise below

We strongly recommend writing the questions and your workings down onto paper as you progress. iPad or tablet users should hold it in portrait. Try here if experiencing problems.

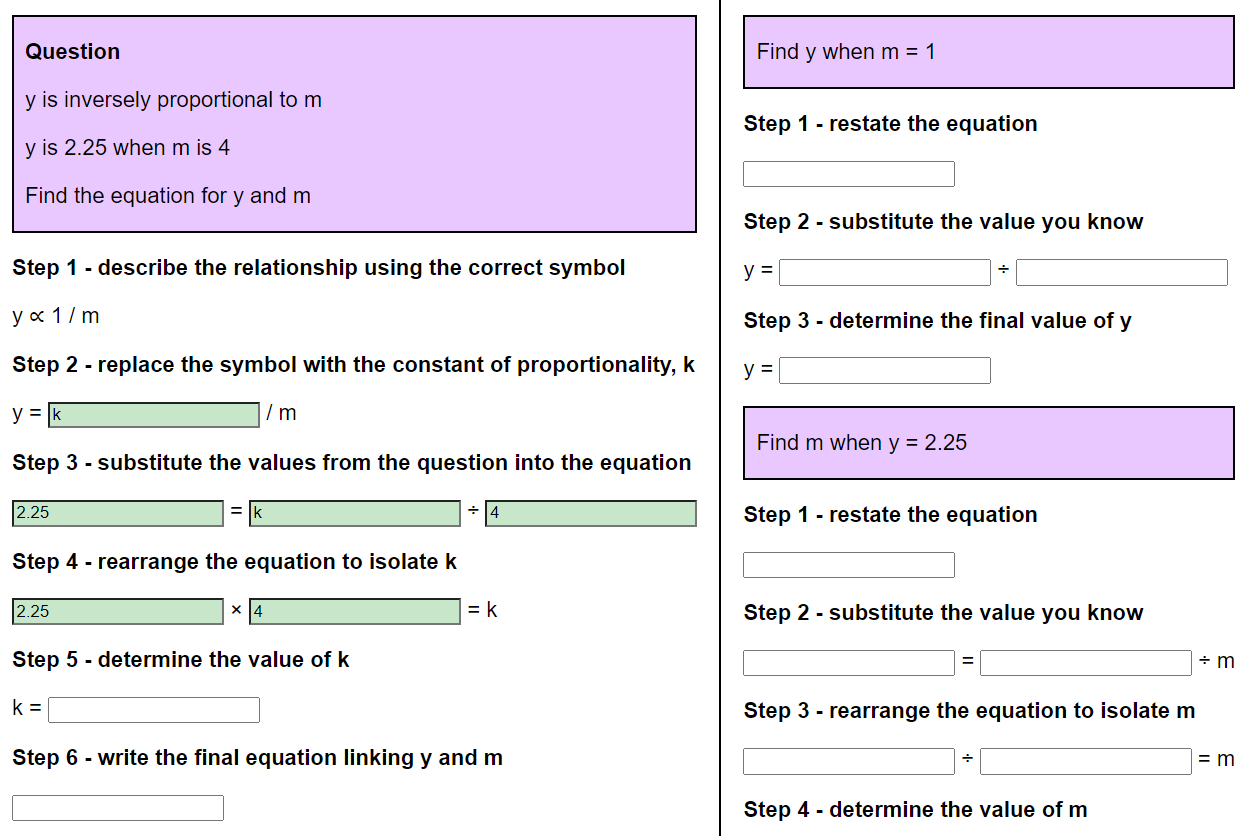
Question

y is inversely proportional to m

y is when m is

Find the equation for y and m

Step 1 - describe the relationship using the correct symbol

y ∝ 1 / m

Step 2 - replace the symbol with the constant of proportionality, k

y = / m

Step 3 - substitute the values from the question into the equation

= ÷

Step 4 - rearrange the equation to isolate k

× = k

Step 5 - determine the value of k

k =

Step 6 - write the final equation linking y and m

Find y when m =

Step 1 - restate the equation

Step 2 - substitute the value you know

y = ÷

Step 3 - determine the final value of y

y =

Find m when y =

Step 1 - restate the equation

Step 2 - substitute the value you know

= ÷ m

Step 3 - rearrange the equation to isolate m

÷ = m

Step 4 - determine the value of m

m =

Score: 0